數學家發現了愛因斯坦瓦片，它可以無限鋪滿一個平面而不會重復

:0:1

數學家們發明了一種新的13邊形，可以無限地鋪滿一個平面，而不會出現重復的圖案。他們稱之為「愛因斯坦瓦片」。這個詞并不是來自著名的物理學家阿爾伯特·愛因斯坦，而是來自他姓氏的德語翻譯：一塊石頭。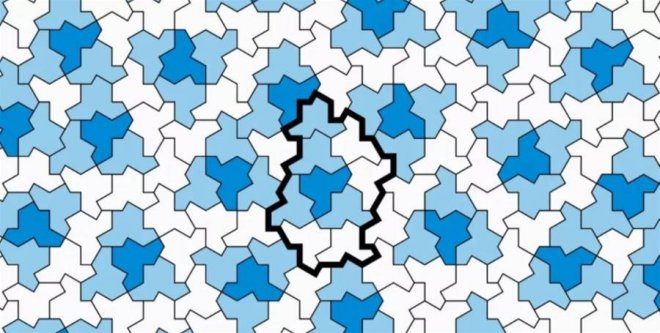

數學家們對這個問題感興趣已經有幾十年了。早在1961年，數學家王浩就提出了一個猜想，認為無周期平鋪，即永遠不會成為重復圖案的平鋪，是不可能的。但他自己的學生羅伯特·伯格爾卻證明了他錯了，他找到了一組20，426個形狀，當仔細排列時，永遠不會重復。
他後來將這個集合縮減到了104個瓦片。這意味著如果你買了一套這樣的瓦片，你可以把它們排列在你的廚房地板上，永遠不會找到一個重復的圖案。

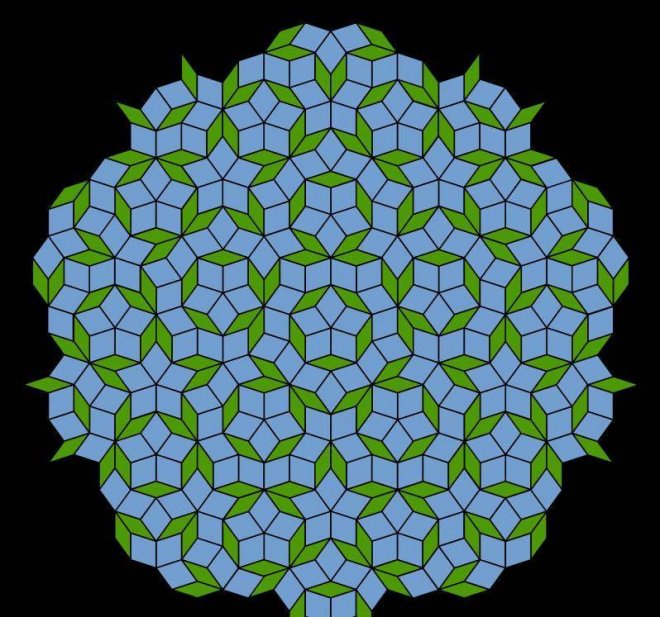
彭羅斯平鋪包含多種對稱性，但它永遠無法周期性重復。
在20世紀70年代，諾貝爾獎獲得者、物理學家羅杰·彭羅斯發現了一組只有兩個瓦片的集合，它們可以以非重復的方式排列在一起，現在被稱為彭羅斯平鋪。
從那時起，世界各地的數學家們都在尋找無周期平鋪的圣杯，「愛因斯坦瓦片」。他們是否能找到一種單一的形狀能夠填充一個二維空間，而不會重復它所創造的圖案呢？
答案剛剛被英國東約克郡一位退休印刷技術員大衛·史密斯發現了。他是如何發現這個驚人的解決方案的呢？「我總是在擺弄和實驗各種形狀，」史密斯告訴《紐約時報》。

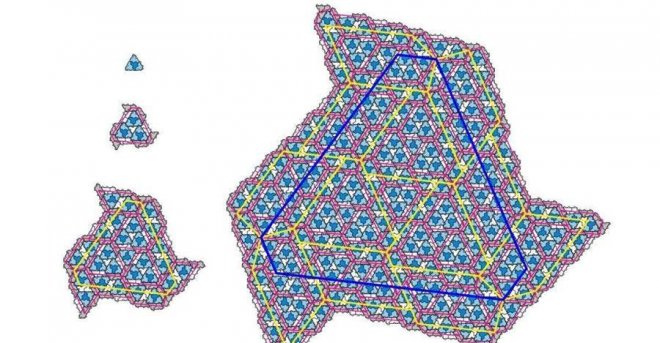
史密斯發現了一個13邊形（也稱為十三角形），它有一個特殊的性質：它可以被分成四個更小的相同形狀（稱為子瓦片），或者可以被組合成四個更大的相同形狀（稱為超級瓦片）。這意味著這個13邊形可以無限地縮小或放大，并且可以用來鋪滿一個平面，而不會出現重復的圖案。這就是「愛因斯坦瓦片」的定義。
史密斯的發現是數學界的一個重大突破，也是一個美麗的藝術作品。他的13邊形有著復雜而優雅的對稱性，可以創造出令人驚嘆的圖形。他還給他的形狀起了一個有趣的名字：帽子，因為它看起來像一個戴著帽子的人的輪廓。
史密斯并不是一個專業的數學家，但他對形狀和圖案有著濃厚的興趣。他曾經設計過一種新型的拼圖，叫做「史密斯拼圖」，它由一些不規則的形狀組成，可以拼成任何你想要的圖案。他還曾經發明過一種新型的骰子，叫做「史密斯骰子」，它由一些不同形狀的多面體組成，可以用來玩各種游戲。

史密斯說，他對「愛因斯坦瓦片」的靈感來自于一本關于無周期平鋪的書籍，以及一些網上的資源。他用電腦軟件來設計和測試他的形狀，并與一些數學家和藝術家交流他的想法。他說，他花了大約兩年的時間才找到了這個13邊形，并證明了它是一個「愛因斯坦瓦片」。
史密斯說，他對自己的發現感到非常興奮和自豪。「我覺得我做了一件很特別的事情，」他說，「我覺得我創造了一種新的美。」

史密斯和他的合作者們已經將他們的發現發表在了數學雜志《幾何與拓撲》上，并得到了其他數學家們的認可和贊揚。他們還計劃制作一些實體模型，以展示他們的形狀在三維空間中是如何排列和變化的。
史密斯說，他希望他的發現能夠激發更多人對數學和藝術之間的聯系感興趣，并且能夠為未來可能有用的應用打開新的可能性。「我認為這是一個很有價值和有趣的領域，」他說，「我希望能夠繼續探索和創造更多。」

[圖擷取自網路，如有疑問請私訊]